unit circlw|arctic circle in norway : Bacolod Using the unit circle, the sine of an angle \(t\) equals the \(y\)-value of the endpoint on the unit circle of an arc of length \(t\) whereas the cosine of an angle \(t\) .
NOTE: The instructions that are provided in SWORDS will need to be followed to finalize your financial aid. All communications will be sent through the student's MGA email. Please check your MGA email to monitor the progress of your Financial Aid status and updates, in addition to checking your SWORDS account.
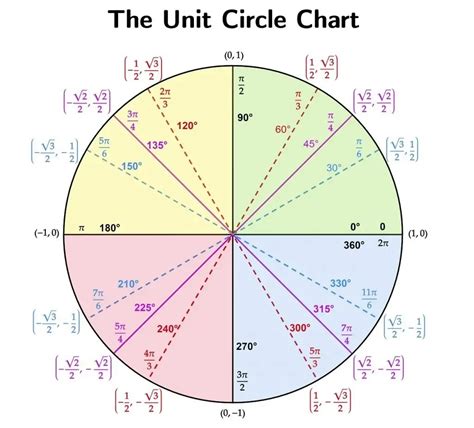
unit circlw,In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as S because it is a one-dimensional unit n-sphere.
Using the unit circle diagram, draw a line “tangent” to the unit circle where the hypotenuse contacts the unit circle. This line is at right angles to the hypotenuse at the unit circle and touches .
Learn what a unit circle is, how to find trigonometric functions using a unit circle, and how to use the Pythagorean identities. See the unit circle chart, examples, and practice . Start practicing—and saving your progress—now: https://www.khanacademy.org/math/alge. Extending SOH CAH TOA so that we can define trig functions for a broader class of angles Practice this .Learn what a unit circle is, how to find its equation, and how to use it to define and evaluate trigonometric functions. See special angles, reference angles, and how to memorize the unit circle values. Using the unit circle, the sine of an angle \(t\) equals the \(y\)-value of the endpoint on the unit circle of an arc of length \(t\) whereas the cosine of an angle \(t\) .

A unit circle is a circle of unit radius, i.e., of radius 1. The unit circle plays a significant role in a number of different areas of mathematics. For example, the functions of trigonometry are most simply defined .What is the unit circle definition of the trigonometric functions? The unit circle definition allows us to extend the domain of sine and cosine to all real numbers. The process for .We “wrap” the number line about the unit circle by drawing a number line that is tangent to the unit circle at the point \((1, 0)\). We wrap the positive part of the number line around the unit circle in the counterclockwise .This equation is known as Pythagorean Identity. It is true for all the values of θ in the unit circle. Using this first Pythagorean Identity, we can find the rest of the Pythagorean Identities. s i n 2 θ + c o s 2 θ = 1. Dividing each .
unit circlwThe general equation of a circle is (x - a) 2 + (y - b) 2 = r 2, which represents a circle having the center (a, b) and the radius r. This equation of a circle is simplified to represent the equation of a unit circle. A unit .
A unit circle has a center at (0, 0) ( 0, 0) and radius 1 1. The length of the intercepted arc is equal to the radian measure of the central angle t t. Let (x, y) ( x, y) be the endpoint on the unit circle of an arc of arc length s s. The (x, y) ( x, y) coordinates of this point can be described as functions of the angle.The unit circle is a circle of radius 1 unit that is centered on the origin of the coordinate plane. The unit circle is fundamentally related to concepts in trigonometry. The trigonometric functions can be defined in terms of the unit circle, and in doing so, the domain of these functions is extended to all real numbers. The unit circle is also related .
In Summary. The unit circle is a fundamental concept in mathematics, specifically in trigonometry. It is a circle with a radius of 1 unit, centered at the origin of a coordinate plane. The unit circle is often used to help understand and visualize the relationships between angles and their corresponding trigonometric functions. A unit circle is a circle of unit radius, i.e., of radius 1. The unit circle plays a significant role in a number of different areas of mathematics. For example, the functions of trigonometry are most simply defined using the unit circle. As shown in the figure above, a point P on the terminal side of an angle theta in angle standard position measured along . 150\degree 150°. As we learned before – sine is a y-coordinate, so we take the second coordinate from the corresponding point on the unit circle: \qquad \sin (150\degree) = \frac {1} {2} sin(150°) = 21. Alternatively, enter the angle 150° into our unit circle calculator. We'll show you the \sin (150\degree) sin(150°) value of your y .unit circlw arctic circle in norwayThe Unit Circle. The point of the unit circle is that it makes other parts of the mathematics easier and neater. For instance, in the unit circle, for any angle θ, the trig values for sine and cosine are clearly nothing more than sin(θ) = y and cos(θ) = x.Working from this, you can take the fact that the tangent is defined as being tan(θ) = y/x, and then substitute for .
Sine, Cosine and Tangent. Sine, Cosine and Tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: For a given angle θ each ratio stays the same. no matter how big or small the triangle is. Trigonometry Index Unit Circle. Sine, Cosine and Tangent . in a Circle or on a Graph. .

The Four Quadrants of the Unit Circle. A quadrant is a quarter of a circle, so there are 4 of them. The value of sin, cos, and tan stay the same in each quadrant, but the sign changes depending on which quadrant the angle is in. Okay, so you have everything needed to build a complete picture. Unit Circle Chart. Take everything you’ve seen so far:
arctic circle in norwayDefining Sine and Cosine Functions from the Unit Circle. The sine function relates a real number t t to the y-coordinate of the point where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle t t equals the y-value of the endpoint on the unit circle of an arc of length t. t. In Figure 2, the sine is equal to .Unit Circle – Explanation and Examples. The unit circle is a circle in the Cartesian plane centered at the origin and with a radius of 1. This circle is useful for analyzing angles and trigonometric ratios. Typically, the initial .
Defining Sine and Cosine Functions from the Unit Circle. The sine function relates a real number t t to the y-coordinate of the point where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle t t equals the y-value of the endpoint on the unit circle of an arc of length t. t. In Figure 2, the sine is equal to .The Unit Circle Written by tutor ShuJen W. The above drawing is the graph of the Unit Circle on the X – Y Coordinate Axis. It can be seen from the graph, that the Unit Circle is defined as having a Radius ( r ) = 1. Going from Quadrant I to Quadrant IV, counter clockwise, the Coordinate points on the axis of the Unit Circle are:
Trigonometric functions are used as models in a wide variety of fields, including engineering, physics, astronomy, and navigation. For example, engineers might use trigonometric functions to describe vibrations or waves, while astronomers might use them to model the orbits of planets. Practice with our Interpreting trigonometric graphs in .
The answer to this is simple: it is called a unit circle because first of all it is a circle, and second, it has a radius equal to 1. So the unit or unitary part comes from the fact that the radius is 1. In Algebra, Calculus and Analytic Geometry there is the need to use the qualifying "unit", because not all circles deal with are actually unit .Angle measurements start at 0 on the positive $ x$-axis and go counter-clockwise around the “circle” until they are back at 360, as shown in the graphs below. Remember from Geometry that there are 360 degrees (360°) in a circle. When going clockwise from the positive $ x$-axis, angles measurements are negative. Here are some examples. A circle is 360 degrees or 2π radians). The numerators start at 0, beginning at the coordinate (1,0), and count up counterclockwise by 1π. This process will yield 0π/2, 1π/2, 2π/2 and 3π/2. Simplify these fractions to get 0, π/2, π and 3π/2. Fig. 3. Unit circle with four associated angles in radians.
unit circlw|arctic circle in norway
PH0 · unit circle quizlet
PH1 · unit circle printable
PH2 · tangents of the unit circle
PH3 · circle machine company boring bars
PH4 · circle circumscribed about a triangle
PH5 · blank unit circle fill in
PH6 · arctic circle in norway
PH7 · Iba pa